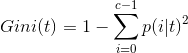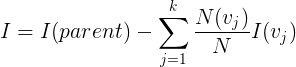Machine Learning in Spark

Implementations and benchmarking of Ordinal Regression and Random Forests from scratch using Apache Spark and pyspark.

Let's get started

Introduction


Spark is a burgeoning big data processing framework that is known to offer fast performance and intuitiveness, through its innovative use of distributed dats structures known as RDDs. On top of Spark sits a library called MLib hosts a wide variety of machine learning algorithms that can be run parallelly on the RDDs. In this project, we chose to tackle two machine learning methods to write: random forests, and ordinal regression. Random forests currently exists within Spark's MLib, but we wanted to see if we could write an implementation that would surpass the performance of MLib's version. Ordinal regression, however, does not exist in MLib. We took it upon ourselves to write both of these algorithms in Spark by leveraging its parallel functionality.

responsive devices

Random Forests


Random Forests are commonly used ensemble learning methods which can be used for classification and regression. The method involves creating a multitude of decision trees during training. For regression we use the mean of the predicted values from all these trees whereas for classification, we use the mode of the predicted values. Random forests are well used in the machine learning community due to them not overfitting.

Decision trees are usually grown deep to gain as much information about the training set as possible. This leads to overfitting of the tree given the data. As the trees are grown deeper they seem to have a lower bias and an increased variance. A low bias implies that the error from the assumptions in the learning model are low. Variance is the error in the modelling caused by sensitivity of the model towards the data. In case of high variance, the noise is modelled as well which leads to erroneous results later on. This is not desirable for a machine learning problem since the test data might not constitute the same distribution as the training set used. An ideal solution is to find the balance between bias and variance since we don’t want our classifier or regressor to be dependent on the data.

The first step towards building many trees was to go ahead and build a single tree. We initially started with the ID3 algorithm and moved to the C4.5 algorithm which are both recursive. The C4.5 algorithm adds support for the continuous variables but the basic algorithm remains the same. We were more interested in implementing this algorithm for classification problems considering the first part of our project dealt with regression.


Building Trees


Both the algorithms we described above are greedy algorithms, which perform locally optimized solutions in the hope of generating a decision tree. The decision tree is built piece by piece by selecting the attribute which had the highest information gain value. Information gain as the name suggests is a measure of the importance of the attribute towards the understanding of the data. It can be measured by comparing the weighted impurity (which in our case is the Gini Impurity) of the child nodes to the impurity of the parent node, where c represents the number of children:



Since for entropy and the information gain we need to be be able to sum over all the classes efficiently. In case of continuous variables, the process of finding the entropy becomes tedious. This slows down the algorithm. Instead the columns which have continuous data have to be binned to create a discrete column. Once the columns have been discretized we are ready to go ahead and carry out training. We also modified the data to keep it in the form of MLib’s labeled point format and hence we always know the location of the target attribute.


ID3 Algorithm


The pseudocode for the ID3 algorithm is as follows:



                        ID3(instances, attributes):
                        	Create a new root node for the tree
                        	If all the instances of the target attribute are same(c):
                        		Return a tree with single root node with the value of the attribute(c)
                        	Else if attributes are empty:
                        		Return a tree with the value of the attribute(c) variable with the highest occurrence in the data
                        	Else:
                        		Find the attribute A which classifies best( highest information gain)
                        		For each value of the variable v belonging to A:
                        			Add a new ramification according to the value A = v
                        			Consider all the instances where A = v
                        			If the instances are empty:
                        				Add a new leaf node with the most common target attribute value.
                        			Else:
                        				Add the subtree given by ID3(instances, attributes)

The tree continues building until the attributes run out or if the information gain after some point turns to be zero. In our case we save the tree as a nested dictionary.


Building Random Forests


To build random forests, we have to build multiple trees. Though we use multiple trees, we need to select only a few columns for building the trees since reducing the columns directly reduces the variance. The data used for training is not the original dataset and a bootstrapped form of the dataset. Hence the process of building trees involves bootstrapping and a randomized selection of columns. Once we have our bootstrapped data we can train our decision trees to get the desired models.


Parallelizing Random Forests

Our basic intuition to parallelizing the problem was to think in two directions. The first method was to store the bootstrapped data in RDD’s and then parallelly create trees. This is a memory intensive method since we have a large amount of bootstrapped data in the RDD’s. This would allow spark workers to parallelly access all the bootstrapped data and create the decision trees. Unlike MLib we do not have an internal tree structure which does not have to be collected in Spark. Hence that will be our biggest cost in the algorithm.


The second method will be to build the tree by using actions and transformations. We managed to get a tree implementation working written only actions and transformations with a very small portion using python functions. The technique works fine for smaller datasets but it’s time consuming in the case of larger datasets. Hence we decided not to go with this approach even when it did have a lower memory footprint for the problem.


Results


We ran our implementation and benchmarked it against MLib's random forest, using the same dataset. As you can see, as we train more trees, the performance doesn't increase due to memory constraints. We extrapolate that our code is 1.5 times slower than MLib as trees increase.

Ordinal Regression


In order to model categorical data, there are two possible approaches: multinomial logistic regression, and ordinal regression. Both of these models extend the popular binary logistic regression to include more than two variables.

In Multinomial logistic regression, the dependent variable $Y$ is modelled taking values in category $c = c_1, ..., c_C$ via $$ \mathbb{P}(Y_i = c_j) = \frac{\exp(\beta_K X_i)}{1 + \sum_{k=1}^K \exp(\beta_k X_i)}$$ Both sklearn and Mlib implement this approach to some extent. That is, sklearn can handle multinomial logistic regression, but uses a lbfgs or newton-cg approach only (no sgd) with support for L2 regularization solely. In Mlib, however, multinomial logistic regression is not always the best model to choose. In the case of ratings, the categories represent ordinal values implying some kind of natural order. In a multinomial logistic regression model this order is not considered, and thus it neglects to differentiate between a '5' from a '4'.

To make up for this missing order, we will explore ordinal regression.


Types of Models


Suppose we are given a response captured by a random variable $Y \in \mathbb{R}$ which, with no loss of generality, can be divided into $K$ different categories $\lbrace 1, ..., R \rbrace $ and can maintain their natural order. Furthermore, the sum of the probabilities of each of the categories equals one.We model the ordinal regression model using binary variables $y_1, ..., y_R$ (i.e. $y_r \sim \mathrm{Ber}(p_r))$, which will be used to transform an ordinal response variable into a binary response. This way, ordinal regression can be seen as an extension to a classical, binary variable model.

For the transformation of the ordinal response to a binary one, there are three different, commonly used approaches(let $r =1, ..., R$):

- Cumulative model: $$ y_r = \begin{cases}1 \quad \quad Y \in \lbrace 1, ..., r \rbrace \\ 0 \quad \quad Y \in \lbrace r+1, ..., K\rbrace\end{cases}$$

- Sequential model: $$ y_r\vert_{\lbrace Y \geq r \rbrace} = \begin{cases}1 \quad \quad Y =r \,\vert\, Y \geq r \\ 0 \quad \quad Y >r \,\vert\, Y \geq r \end{cases}$$

- Adjacent model: $$ y_r\vert_{\lbrace Y \in \lbrace r, r+1\rbrace \rbrace} = \begin{cases}1 \quad \quad Y = r \,\vert\, Y \in \lbrace r, r+1\rbrace \\ 0 \quad \quad Y = r+1 \,\vert\, Y \in \lbrace r, r+1\rbrace \end{cases}$$

The most versatile model of these is the cumulative assuming nothing in particular about the data except the ordinal regression assumptions. The sequential model might be used to model variables for which higher values are more likely to be reached if the lower ones have already occured. A similar argumentation holds for the adjacent model with neighbors.


Cumulative model


The cumulative model (or threshold model) can be deviated assuming a latent, underlying r.v. $\tilde{Y}$ for which the actual, observed variable $Y$ can be seen as somehow rounded.

The link between those variables shall be modelled through $$ \lbrace Y = r \rbrace = \lbrace \theta_{r-1} < \tilde{Y} \leq \theta_r \rbrace$$ for $-\infty = \beta_0 < \beta_1 < ... < \beta_{R-1} < \beta_R = +\infty$ For the latent variable a linear regression model with $x, w \in \mathbb{R^n}$ and a random variable $\epsilon$ is choosen: $$ \tilde{Y} = - x^Tw + \epsilon $$

It follows that

$$ \mathbb{P}(y_r = 1 \vert x, w) = \mathbb{P}(Y \leq r \vert x, w) = \mathbb{P}(-x^Tw + \epsilon \leq \beta_r) = \mathbb{P}(\epsilon \leq \beta_r + x^Tw) = F_\epsilon(\beta_r + x^Tw)$$ $$ \implies \mathbb{P}(Y = r) = F_\epsilon(\beta_r + x^Tw) - F_\epsilon(\beta_{r-1} + x^Tw)$$

using the cdf $F_\epsilon$ of $\epsilon$.

In the model setup the only thing left to define is what distribution to assume/choose for $\epsilon$. Some possible choices which yield different popular models are: thecumulative logit distribution ($ \epsilon \sim \mathrm{Logistic}(0,1)$), the probit distribution($\epsilon \sim \mathcal{N} (0, 1)$), the maximum extreme-value distribution ($ \epsilon \sim \mathrm{Gumbel}(0, 1)$), and the minimum extreme-value distribution: $ -\epsilon \sim \mathrm{Gumbel}(0, 1)$).

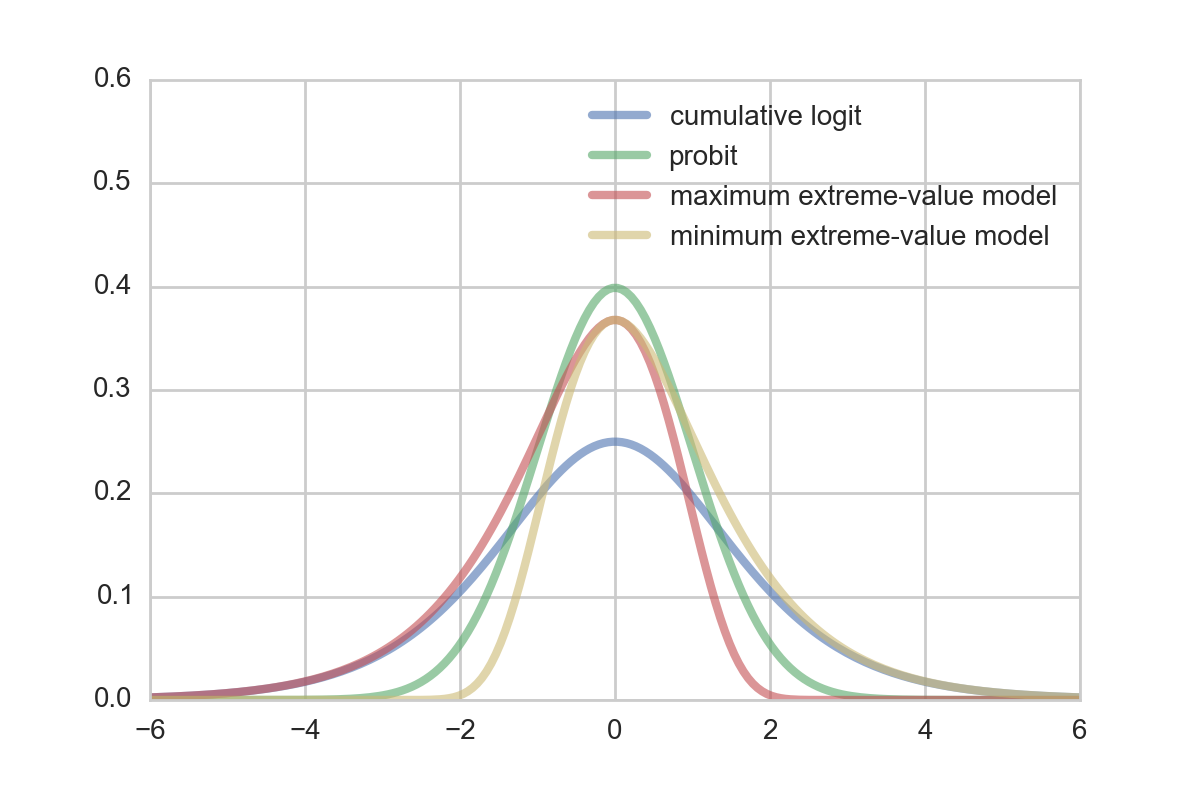
Distributions

Whereas the probit and logit model are a good choice for symmetric errors, the Gumbel and reversed Gumbel distribution can be used for the case of asymmetric error distributions to provide a better fit. For many cases, a certain asymetry regarding the error is quite natural.


Fitting the model


Assume we are given $N$ datapoints $(Y_1, X_1), ..., (Y_N, X_N)$ with $Y_i \in \lbrace 1, ..., R \rbrace, \quad X_i \in \mathbb{R}^L$ (independence assumption as usual). We simplify the fitting process, by using predefined boundaries $\beta$. Of course it is also possible to put a prior on $\beta$ and include it in the optimization approach but to do so, additional constraints need to be satisfied (i.e. $-\infty = \beta_0 < 1 < \beta_1 < 2 < ... < \beta_{R-1} < R < \beta_R = \infty$).

One easy way to define the bounds is to use the middle, i.e. $\beta_r = r - 0.5 \quad \text{for} \quad r = 1, ..., R-1$. Then, the log likelihood function of the data $\mathcal{D} = \lbrace (Y_1, X_1), ..., (Y_N, X_N) \rbrace$ is given as $$ \mathcal{L}(w \; \vert \; \mathcal{D}, \beta) = \sum_{n=1}^N \log \left( F_\epsilon(\beta_{Y_n} + X_n^T w) - F_\epsilon(\beta_{Y_n-1} + X_n^Tw) \right)$$

This allows us to derive a Maximum Likelihood for the model. $$ \hat{w}_{\mathrm{MLE}} = \underset{w}{\operatorname{argmax}} \mathcal{L}(w \; \vert \; \mathcal{D}, \beta)$$ We can also estimate the Maximum a posterior (MAP). The MAP estimate can be derived by ignoring the normalization constant (cf. properties of an argmax) as $$ \hat{w}_{\mathrm{MAP}} = \underset{w}{\operatorname{argmax}} \mathcal{L}(w \; \vert \; \mathcal{D}, \beta) + \log f_w(w)$$ with $f_w$ being the pdf of the choosen prior distribution for $w$. Popular choices are:

- Ridge regression: $w \sim \mathcal{N}(0, \tau I)\quad \quad$ (Gaussian prior with diagonal matrix)

- LASSO regression: $w_i \sim \mathrm{Laplace}(0, \tau)\quad \quad$ (Laplace prior, indep. components)


Implementation


One way to solve the optimization problem is to use stochastic gradient descent. This was chosen over other gradient descent methods such as conjugate-gradient and l-bfgs because for huge amounts of data, the others require either a small step size or an excessive amount of memory. Especially in Machine Learning applications stochastic gradient descent has become one of the default algorithms and was choosen here.

Stochastic gradient descent can be parallelized as described in the famous paper by Zinkevich. In the paper, the authors suggest a simple algorithm which shuffles the data in the array randomly. To optimize the process, each node should node the same amount of data and the gradient is computed over all data. Thus the 'stochasticness' is done mainly in the shuffle step. After each round computation results are aggregated by average.

Though this algorithm intuitively seems to be quite straightforward, the question was open until the paper has been released whether this approach is optimal. In the paper a proof is given that this method converges. Given that there does not exist any parallelization strategy that is able to gain more speedup, the parallelized stochastic gradient is optimal.

However, this is a theoretical result. In our implementation we wanted to see what kind of speedup we could achieve using Spark, and which model gives best accuracy at lowest computational cost.


Computing the gradient


One one the critical steps in any numerical optimization routine is the gradient which is the component that takes most time to evaluate. In our implementation we used autograd (https://github.com/HIPS/autograd), a handy python package for automatic differentation. Especially in the case of ordinal regression, depending on which model has been choosen to present the latent variabel $\tilde{Y}$, the gradient might be not trivially deviated.

General Gradient

Here, an outline of computing the gradient of a simple model given $n$ datapoints is given: $$ \begin{split} \frac{\partial \mathcal{L}(w \;\vert\; \mathcal{D}, \beta )}{\partial w_j} &= \frac{\partial}{\partial w_j} \sum_{i=1}^n \log \left( F_\epsilon\left( \beta_{Y_i} + X_i^Tw \right) - F_\epsilon\left( \beta_{Y_i - 1} + X_i^Tw \right) \right) \\ &= \sum_{i=1}^n \frac{\partial}{\partial w_j} \log \left( F_\epsilon\left( \beta_{Y_i} + X_i^Tw \right) - F_\epsilon\left( \beta_{Y_i - 1} + X_i^Tw \right) \right) \\ &= \sum_{i=1}^n \frac{\frac{\partial}{\partial w_j}\left[ F_\epsilon\left( \beta_{Y_i} + X_i^Tw \right) - F_\epsilon\left( \beta_{Y_i - 1} + X_i^Tw \right) \right]}{F_\epsilon\left( \beta_{Y_i} + X_i^Tw \right) - F_\epsilon\left( \beta_{Y_i - 1} + X_i^Tw \right)} \\ &= \sum_{i=1}^n \frac{f_\epsilon\left( \beta_{Y_i} + X_i^Tw \right)X_{i,j} - f_\epsilon\left( \beta_{Y_i - 1} + X_i^Tw \right)X_{i,j}}{F_\epsilon\left( \beta_{Y_i} + X_i^Tw \right) - F_\epsilon\left( \beta_{Y_i - 1} + X_i^Tw \right)} \\ &= \sum_{i=1}^n \frac{f_\epsilon\left( \beta_{Y_i} + X_i^Tw \right) - f_\epsilon\left( \beta_{Y_i - 1} + X_i^Tw \right)}{F_\epsilon\left( \beta_{Y_i} + X_i^Tw \right) - F_\epsilon\left( \beta_{Y_i - 1} + X_i^Tw \right)}X_{i,j} \\ &= \sum_{i=1}^n g(\beta, X_i, Y_i)X_{i,j} \\ \end{split} $$ With $X_{i,j}$ being the $j$-th component of the vector $X_i$ and $f_\epsilon$ being the density of $\epsilon$.


Analysis


As adding a prior add only a constant time factor to the model computation, for our analysis we did not focus whether the model produced actual, meaningful values (which might requires several hours - days to train for) but instead how the performance for a small subsample (2000 samples) behaved for each error type. Also, as we used more variables than data points extreme overfitting was taken into account. Thus, though not completely correct we can at some point roughly take accuracy / RMSE as some sort of measure of how fast a model adjusts.

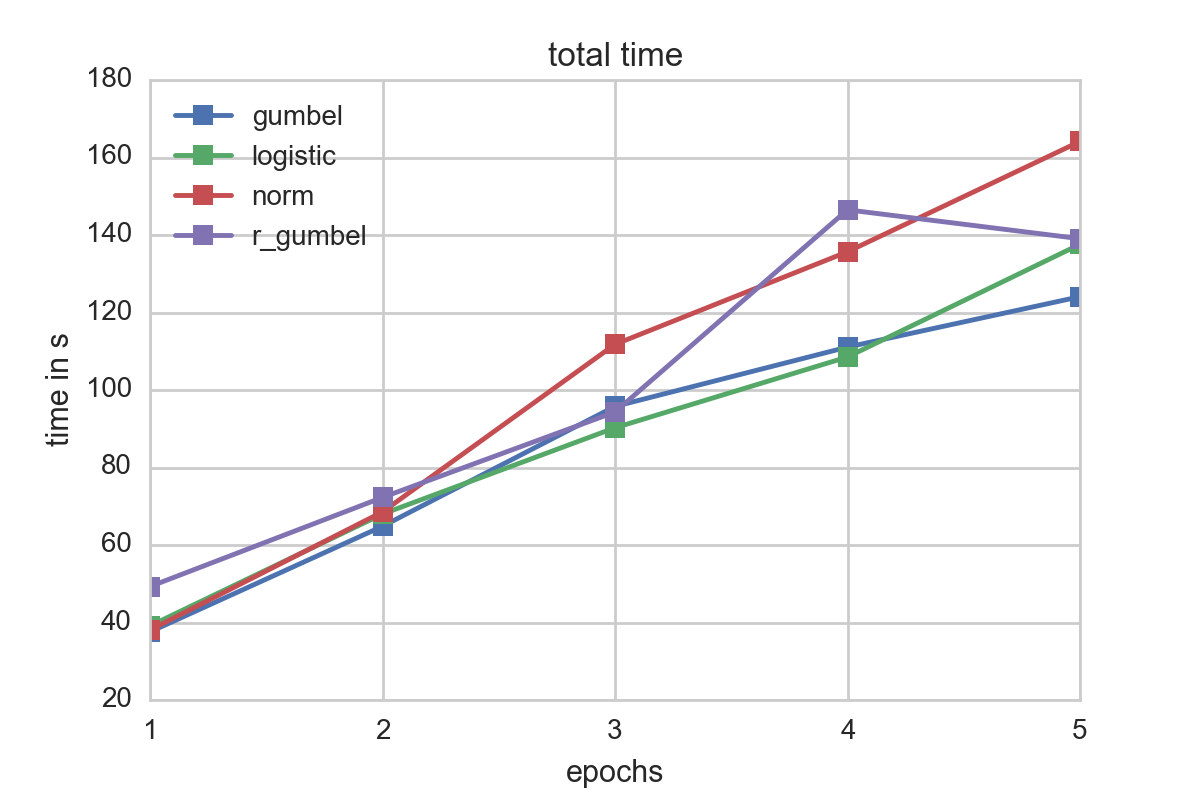
For our testsample, logistic and gumbel errors seemed to perform best in terms of fitting times. A look at the time spent per epoch underscores this:

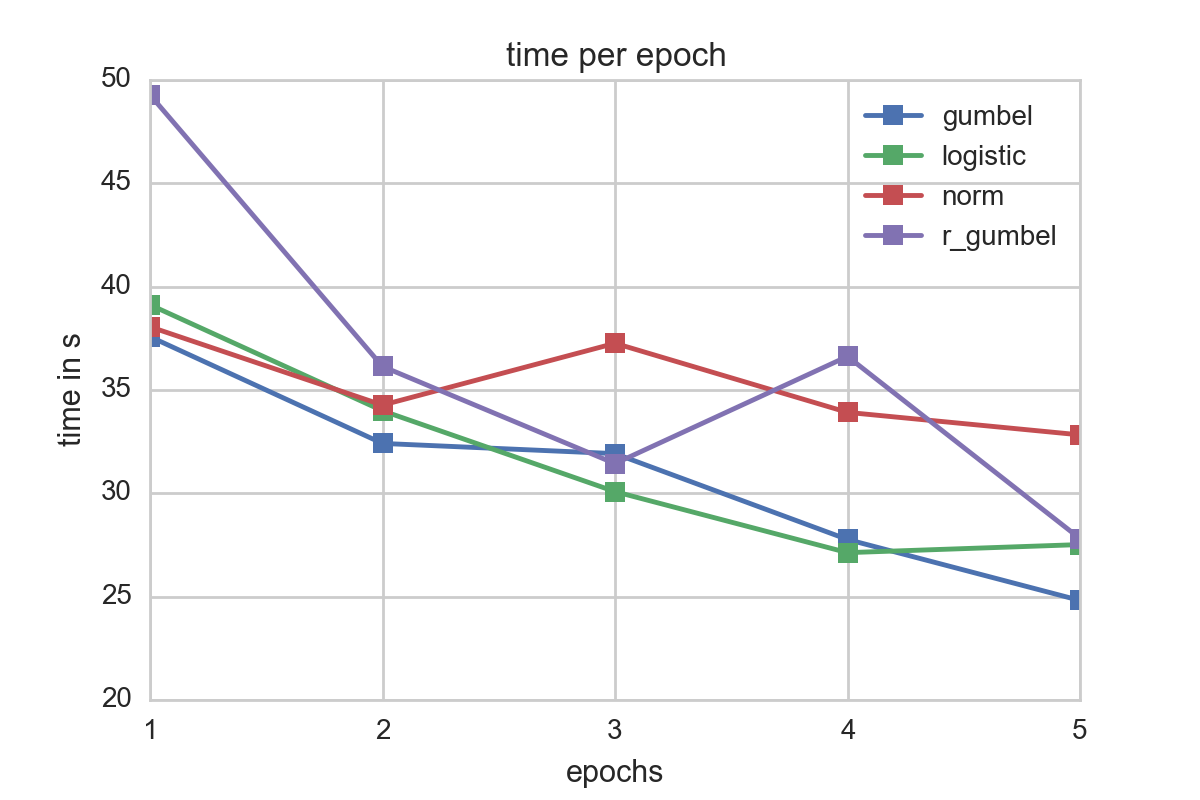
It is also worth noting thatthe time per epoch increases for all error distributions when the number of epochs increase. This might be due to amortization of the Spark overhead and also internal Spark caching effects.

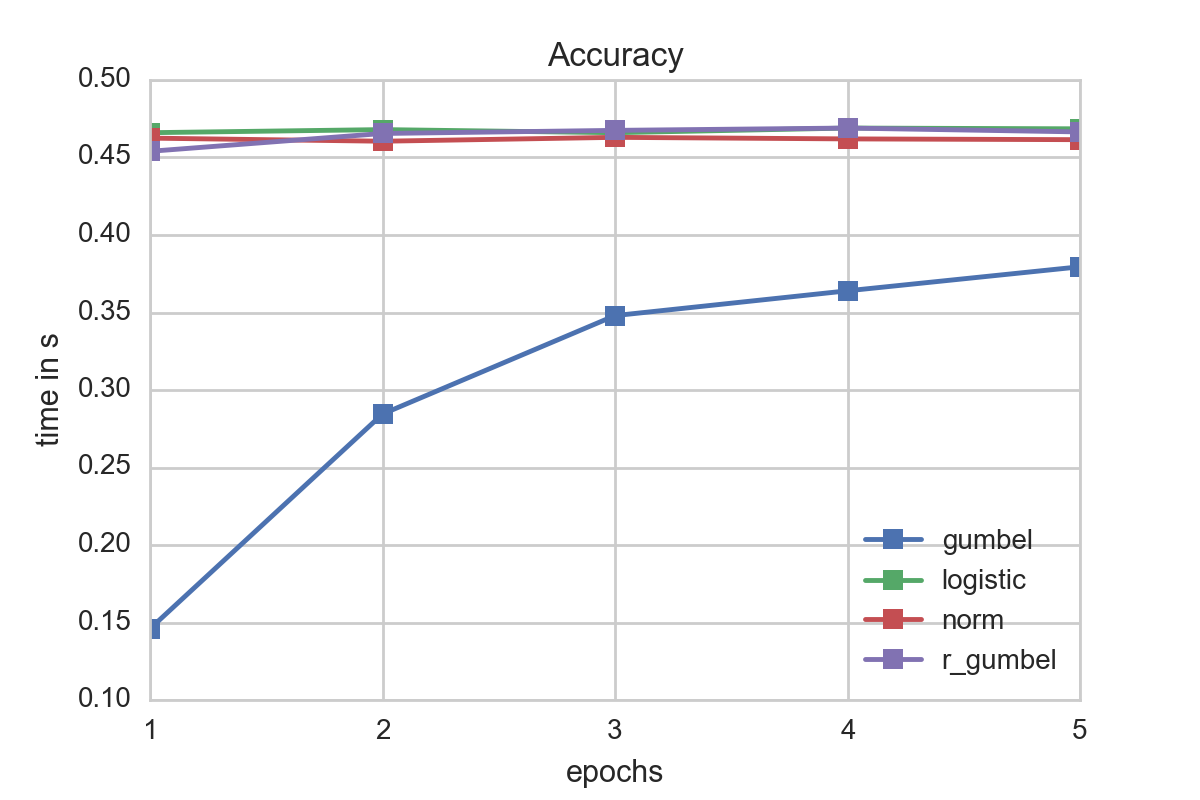
Though in terms of speed the gumbel distribution seemed to be favorable, a quick a look at the accuracy reveals that the other models matched for the given data better. Our recommendation is therefore to use as a first start a logistic ordinal regression model. However if information about the data or its errors are known it might be a good idea to fit a Gumbel distribution as its evaluation is faster than the logistic one which might be to due to the lack of the division operator.


Team

Neil Chainani

Github: nchainan

Abhishek Malali

Github: abhishekmalali

Leonhard Spiegelberg

Github: LeonhardFS